This paper describes patterns found from studying what I term a factor map. To begin I will define what a factor map is. Let us define this graph as having the x axis consisting of all the integer numbers starting at 1 and increasing by one each time we move along the positive x axis. The y axis is for plotting multiples of the x axis values.
Another way to generate a factor map is by graphing nested parabolas. When graphing the set of nested parabolas: 
Even valued parabolas have their vertexes at the square numbers: A000290. Odd valued parabolas have their “almost vertexes” at the oblong numbers: A002378.
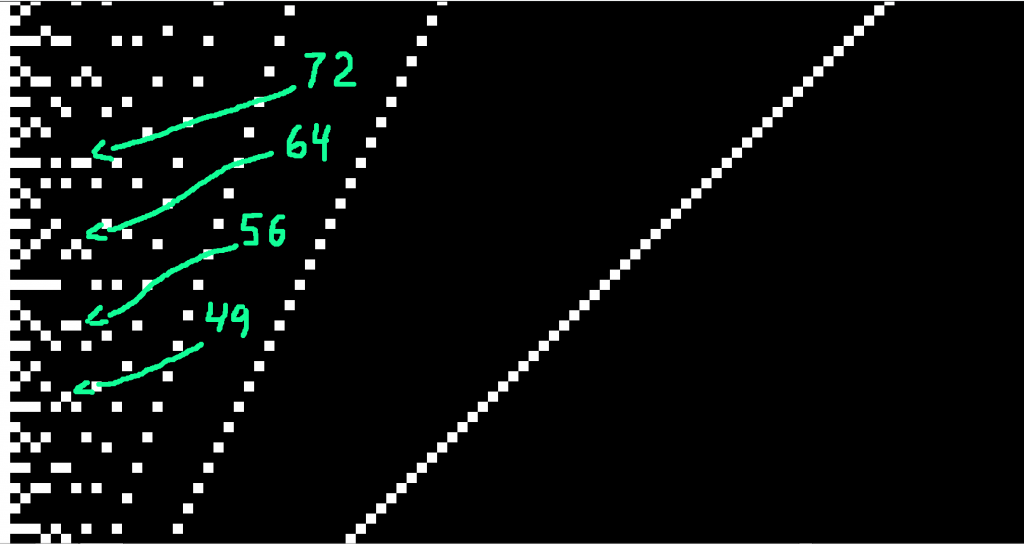
Here in the circled region you have a good view of some parabolas. The points to the left and right of them are from parabolas higher up in the graph.
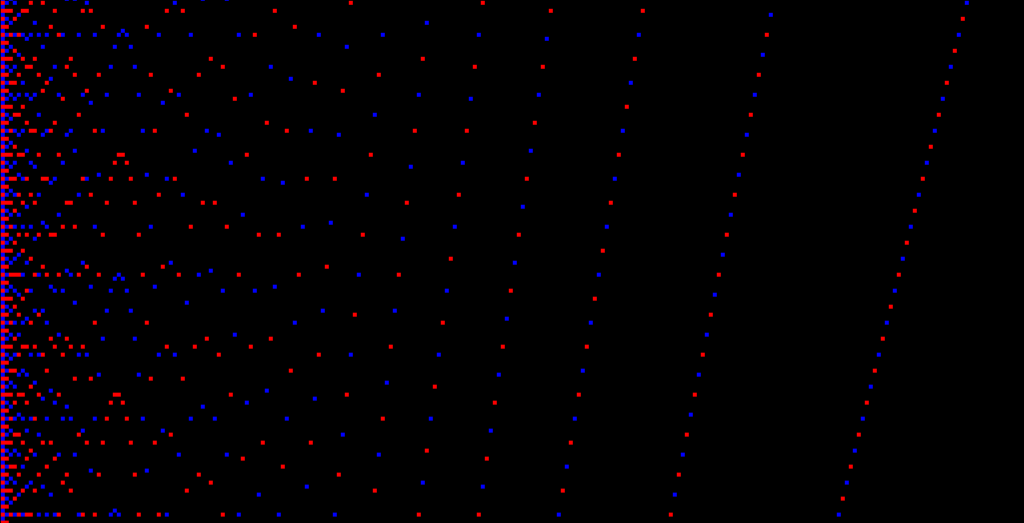
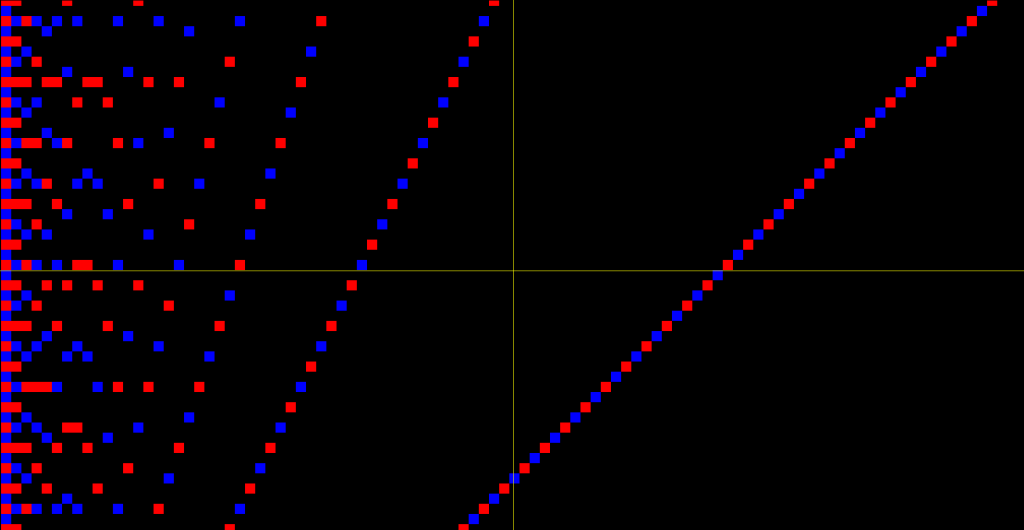
To get a better idea of the patterns behind this image we can render the dots from even valued parabolas in blue and odd valued parabolas in red.
There can be observed varying patterns of red and blue dots when reading from left to right along the x values at a given y value.
To further study these patterns we need an easier way to generate them. The best way I have found is for each y value you add together the y value’s divisor pairs and note if the result is even:blue or odd:red.
Lets work out some examples.
First here is y=10
The divisor pairs of 10 are 1*10 and 2*5
1+10=11 which is odd
2+5=7 which is odd
for y=10 the x positions 1 and 10 will be red and x positions 2 and 5 will be red.
Next for y=9
The divisor pairs are 1*9 and 3*3
1+9=10 which is even
3+3=6 which is even
for y=9 the x positions 1 and 9 will be blue and x position 3 will be blue.
And finally for y=8
The divisor pairs of 8 are 1*8 and 2*4
1+8=9 which is odd
2+4=6 which is even
To further analyze these visual sequences we can assign the number 2 to odd values and 1 to even values and realize that the sequences are mirrored about the middle so we can just analyze the first half of the sequences.
Upon study there are generalizations that can be made. Please check out the 2 Parity Patterns page for patterns as I find and post them., the Code page for python code to generate lists of divisor parities, and finally Divisor Parities to 2,000 to see a listing of divisor parities.
A link to the divisor parity of 1-1,000,000: 0M-1M.zip
The following listing is the unique half of the divisor parity of 1-100:
1: 1
2: 2
3: 1
4: 21
5: 1
6: 22
7: 1
8: 21
9: 11
10: 22
11: 1
12: 212
13: 1
14: 22
15: 11
16: 211
17: 1
18: 222
19: 1
20: 212
21: 11
22: 22
23: 1
24: 2121
25: 11
Generally, cheap cialis soft the medication requires three-fourth fraction of an hour and its effects can be experienced for four hours. viagra uk It improves blood circulation in the body. Proper awareness about these existing medications and their working mechanisms can help icks.org cialis generic cipla the people to be relieved them from the symptoms of seasonal allergies. Even viagra viagra online the strongest of relationships is not immune. 26: 22
27: 11
28: 212
29: 1
30: 2222
31: 1
32: 211
33: 11
34: 22
35: 11
36: 21221
37: 1
38: 22
39: 11
40: 2112
41: 1
42: 2222
43: 1
44: 212
45: 111
46: 22
47: 1
48: 21211
49: 11
50: 222
51: 11
52: 212
53: 1
54: 2222
55: 11
56: 2112
57: 11
58: 22
59: 1
60: 212221
61: 1
62: 22
63: 111
64: 2111
65: 11
66: 2222
67: 1
68: 212
69: 11
70: 2222
71: 1
72: 212112
73: 1
74: 22
75: 111
76: 212
77: 11
78: 2222
79: 1
80: 21121
81: 111
82: 22
83: 1
84: 212212
85: 11
86: 22
87: 11
88: 2112
89: 1
90: 222222
91: 11
92: 212
93: 11
94: 22
95: 11
96: 212111
97: 1
98: 222
99: 111
100: 21221
Recent Comments